个位上数是1，十位上数是3，这个数是（）

A.① 36

B.② 63

C.③ 25

A.97

B.67

C.76

A.881

B.188

C.818

A．4

B．13

C．15

D．18

设a₁，a₂，...，a_n是n个不同的数，而F(x)=(x-a₁)(x-a₂)...(x-a_n)，b₁，b₂，...，b_n是任意n个数，显然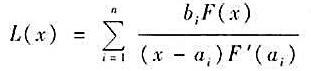适合条件L(a_i)=b_i，i=1，2，...，n。这称为拉格朗日(Lagrange)插值公式。

利用上面的公式求：

1)一个次数＜4的多项式f(x)，它适合条件：f(2)=3，f(3)=-1，f(4)=0，f(5)=2。

2)一个二次多项式f(x)，它在x=0，2/π，π处与函数sinx有相同的值。

3)一个次数尽可能低的多项式f(x)，使f(0)=1，f(1)=2，f(2)=5，f(3)=10。

A.51

B.58

C.65

【题目描述】

第 44 题有这样的两位数，它的两个数字之和能被4整除，而且比这个两位数大1的数，它的两个数字之和也能被4整除。所有这样的两位数的和是多少（）

符合条件的两位数的两个数字之和能被4整除，而且比这个两位数大1的数.若十位 数不变，则个位增加1，其和便不能整除4，因此个位数一定是9，这种两位数有39、79。所以所求的和是39+ 79=118。

【我的疑问】（如下，请求专家帮助解答）

寻详解

inti，j，x，y；

for（i=10；i＜100；i++）

{

x=i%10；

y=i/10；

J=（）；

if（（））

System.out.print（i+""）；

}

A.10238

B.21228

C.21048

A.第一个适宜稀释度平板上的菌落数

B.指常数2

C.适宜范围菌落数的第一稀释度(低)平板个数

D.稀释因子

A.扩大到原数的10倍

B.缩小到原数的1/10

C.扩大到原数的100倍

D.缩小到原数的1/100